The role gallium-nitride FETs play in the design of an EV charging circuit help illustrate how these wide-bandgap semiconductors facilitate energy efficiency.

FENG QI, TRANSPHORM
THE PHASE-SHIFT FULL BRIDGE (PSFB) is a classic topology for applications that must accommodate a wide range of operating voltages, as with battery chargers. A PSFB converter generally uses four power switches (MOSFETs or IGBTs) to form a full bridge on the primary side of an isolation transformer. Diode rectifiers or MOSFET switches perform synchronous rectification on the secondary side. A phase shift between PWM signals driving the two legs of the full bridge determines how much energy gets transferred to the load. A control algorithm manipulates this phase shift to regulate and maintain the output voltage at the desired level. An attraction of this topology is that it permits zero-voltage switching (ZVS) of its switching devices. This lowers switching losses and makes the converter efficient.

An advantage of this circuit over an LLC topology is that it does not need either a variable switching frequency or a variable dc-link voltage to regulate the battery voltage. However, there is one imperfection in PSFBs: soft switching is possible at high loads, but the devices inevitably enter hard switching under low loads.

It can be particularly advantageous to devise PSFBs with GaN FETs rather than with traditional silicon power devices. Reasons include the ability to realize a higher switching frequency and a higher power density, and the topology can work at a larger phase-shift angle at high efficiency. The soft-switching region is also larger, and when hard switching is necessary, the losses are lower. These benefits result from a low output charge (Q_oss) and low switching losses in the GaN power devices.

To further improve efficiency, an active snubber can replace the conventional RCD snubber. The snubber is necessary to squelch secondary parasitic ringing that arises with high output voltages. Without some kind of a snubber, the ringing would put a lot of voltage stress of the rectifier diodes. A traditional RC damping snubber isn’t practical because it is lossy in high-voltage high-frequency applications. An RCD clamped snubber circuit is generally added to keep the secondary voltage down.

In one case, a prototype PSFB employed the 72-mΩ Transphorm GaN FET (TPH3212PS). Its total resonant inductance is about 2.7 µH and arises from the combination of leakage and resonant inductance. This resonant inductance allows di/dt as high as 150 A/µsec with a 410-V dc-link. The high di/dt significantly increases the maximum phase-shift angle, reducing power loss caused by the freewheeling time. This trick can easily push the angle over 0.9π (the higher the angle, the less free-wheeling time required). The high phase angle allows the turns-ratio of transformer to be reduced and further improves the efficiency.

Using this technique a 450-V battery can be charged with a 410-V dc-link and 0.93π phase shift. The high di/dt lets the circuit reach 26 A of current in 175 nsec at a power level of 3,600 W.

The voltage spike on the output (V_rec in the nearby figure labeled Plots of I_L1 and V_rec) is clamped to around 540 V by the active snubber. The snubber is controlled with offline converter ICs such as the STMicroelectronics VIPER06HS or ON Semiconductor NCP1060AD100. The active snubber has three terminals connected across V_rec and V_o. It is composed of two parts, an input filter and switcher cells.

In the simplified schematic of the active snubber, the switcher, S1, is configured to work with a constant peak current. In this design, the snubber is comprised of three switcher cells and can pump 100 mA depending on the requirement from the parasitic capacitance of the transformer and rectifiers on the secondary side. The junction capacitance of D0 in the active snubber schematic also contributes to the parasitic capacitance. In this design, the four rectifying secondary diodes are 650-V SiC Schottky SCS210 devices, and D0 is a SCS206 diode. By tuning the compensation resistor in the switcher circuits, the overshoot caused by the parasitic components can be clamped at a desired Vrec. The dead time must be less than 175 nsec to give a 0.93π phase shift.

Switching details

In the simplified PSFB schematic, Q1 and Q2 are the leading phase leg, which starts its transition before power transfer. Q3 and Q4 are the lagging phase leg, which starts its transition after power transfer. I_L1 is always higher at the end of power transfer, so it is always easier for the lagging leg to soft switch. In other words, the leading leg loses soft switching at higher power than does the lagging leg.

Insight into the circuit operation comes from examining the switching transition after Q1 has turned-off for both soft and hard switching. Consider an ideal soft switching waveform along with a simplified circuit diagram as depicted nearby (labeled Ideal soft-switching waveform). Q1 turns off at t₁, and Q2 turns on at t₂. There is a zero-voltage soft switching transition during the dead time t_db. During this process, C_oss of Q1 charges from 0 V to Vdc, and C_oss of Q2 is discharged from Vdc to 0 V. In other words, Q_{oss_0ToVdc} and E_{oss_0ToVdc} are injected in Q1, and Q_{oss_VdcTo0} and E_{oss_VdcTo0} are removed from Q2. Meanwhile, Q_{oss_VdcTo0 x Vdc} are energized to the level of the dc-link because the discharging current of Q2 flows through the dc-link. The process is powered by the inductor current, I_L1. Equations (1) and (2) give the relationship between I_L1 and the charge and energy during the transition.

I_{L1_1} is the current at t₁, and I_{L1_2} is the current at t₂. In (2), average current during the transition is approximated by the arithmetic mean, which is smaller than the actual value.

If there is no restriction on t_db, the minimum I_{L1_1} to maintain soft switching happens when I_{L1_2} is 0 A. If t_db is targeted to a value, such as 87.5 nsec in this case, the minimum I_{L1_1} can also be derived from the equations. The corresponding values are calculated at a 400-V dc-link. They define the boundary between soft switching and hard switching. When I_{L1_1} is lower than the boundary values, Q1 and Q2 start hard switching. Assuming Q2 is turned on with V_x remaining on its drain, the nearby figures give the waveform and simplified circuit diagram for two typical cases of hard switching.

For both cases, before turn-on of Q2, Q_{oss_0To(Vdc-Vx)}, has charged to Q1, and/or Q_{oss_VdcToVx}, has been discharged from Q2. Correspondingly, E_{oss_0To(Vdc-Vx)} has been stored in Q1, E_{oss_VdcToVx} has been removed from Q2, and Q_{oss_VdcToVx x Vdc} has been stored in the dc-link. In other words, Q_{oss_(Vdc-Vx)ToVdc} will be charged into Q1 during the turn-on of Q2.

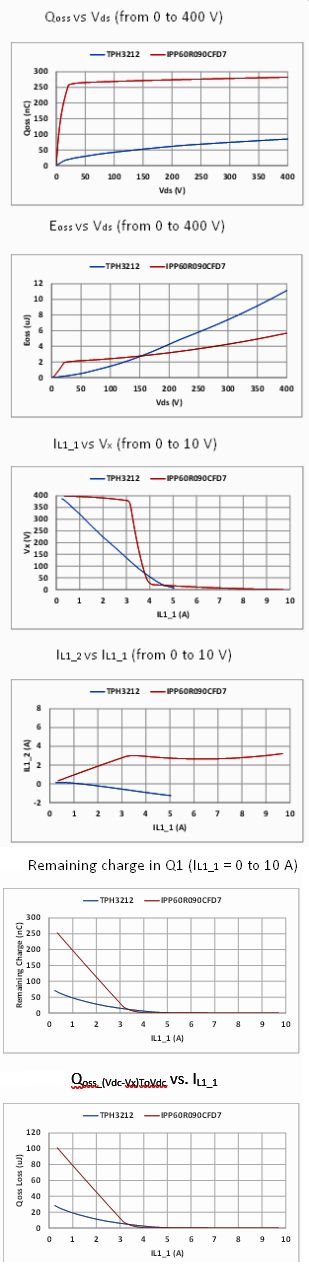
The build-up of the remaining charge causes turn-off loss in Q1, E_{oss_VxToVdc}, and turn-on loss in Q2, Vdc x _{Qoss_(Vdc-Vx)ToVdc} – E_{oss_VxToVdc}. On the other hand, the turn-on of Q2 also suffers from losses caused by I_{L1_2}, which is left out of this discussion. For both cases, equations (1) and (2) can be rewritten as equations (3) and (4) by simply replacing the Q_oss and E_oss and assigning 87.5 nsec to the dead time, t_db. Because Q_oss and E_oss are voltage dependent, the following analysis is calculated with the C – V curve instead of C_o(tr) or C_o(er) defined at fixed voltages. With an experimental C – V curve, Q_oss vs. V_ds and E_oss .vs V_ds curves of devices are calculated and shown in a nearby figure (labeled Q_oss vs. V_ds and E_oss .vs V_ds ). Curves for V_x vs. I_{L1_1} and I_{L1_2} vs. I_{L1_1} are calculated with (3) and (4) in another figure (labeled V_x vs. I_{L1_1} and I_{L1_2} vs. I_{L1_1}).

From V_x vs. I_{L1_1}, it is worth noting that V_x of both GaN and Si stay below 50 V at an I_{L1_1}

higher than 4 A. Once I_{L1_1} becomes less than 4 A, the V_x of GaN rises gradually whereas that of Si jumps dramatically and becomes steady around 400 V. This difference can be explained by the Q_oss – V_ds curve. The charge of GaN is more uniformly distributed across the whole voltage range whereas most of the Si charge resides in the low voltage region. From I_{L1_2} – I_{L1_1,} as can be expected, for GaN, a t_db longer than the transition time required by the minimum I_{L1_1} will make V_x slightly pass the valley of Q2 V_ds and end up with a negative I_{L1_2}. If fine-tuning of t_db can be practically implemented in nanoseconds, V_x would be able to stay right at the valley of Q2 V_ds. As for Si, Q2 will be turned on around 3 A I_{L1_2} from 10 A to 3 A I_{L1_1}.

The remaining charge in Q1, Q_{oss_(Vdc-Vx)ToVdc}, and the loss of a phase leg caused by it, V_dc x Q_{oss_(Vdc-Vx)ToVdc}, are presented in a nearby image. As discussed above, this loss is distributed in Q1, E_{oss_VxToVdc}, and Q2, Vdc x Q_{oss_(Vdc-Vx)ToVdc} – E_{oss_VxToVdc}. It is obvious that GaN significantly reduces the remaining charge and the loss caused by it, especially in light load conditions with I_{L1_1} lower than 3 A. At 1 A I_{L1_1}, the loss caused by the remaining charge of GaN is only 25% of that of Si. In other words, GaN cuts 75% of the need for heat dissipation and improves power density by eliminating the need for a significant portion of heat sinking normally needed for Si.

The PSFB is tested across a battery voltage range from 250 to 450 V and in different load conditions.

The efficiency of the PSFB rises with rising battery voltage or phase shift angle and it is above 96% over the whole battery voltage range from 250 to 450 V. Notably, the arithmetic mean of efficiency is above 97% from 250 to 450 V. Converter efficiency is still around 90% at only 10% load. Benefiting from extremely low switching loss, the GaN devices generate a minimal amount of heat and cause little temperature rise during hard switching at 10% load.

References
Transphorm charger design guide