The behavior of a transimpedance amplifier relates directly to the performance of its power supply. Here a low-dropout design with a high power-supply-rejection-ratio can help.
Xavier Ramus,
Product definer, Linear Regulator and Supervisors group
Texas Instruments Inc.
Transimpedance amplifiers (TIA) are used in many applications, from automotive collision avoidance light detection and ranging (LIDAR) systems to optical head-end in fiber optic communication systems. Each system has its own set of requirements such as gain and bandwidth. It is difficult to achieve both high gain and high bandwidth while maintaining good signal-to-noise ratio (SNR). Noise, whether white or due to transient in the power supply, can affect the SNR of the TIA and degrade system performance. This article describes design considerations when designing or specifying the power chain.
Six main parameters define how to find the best power chain for a TIA: output voltage, output current, line regulation, load regulation, output noise and power supply rejection ratio (PSRR).
Before starting the noise analysis on the power chain and its impact on the signal chain, consider that all issues on the signal chain have been resolved and that the performance achieved with a lab power supply are satisfactory. The signal chain selected in our example (Figure 1) consists of a high-performance transimpedance amplifier (OPA857) followed by a fully differential amplifier (THS4521). From this point forward, we will only look at the OPA857 or TIA and power supply parameters.
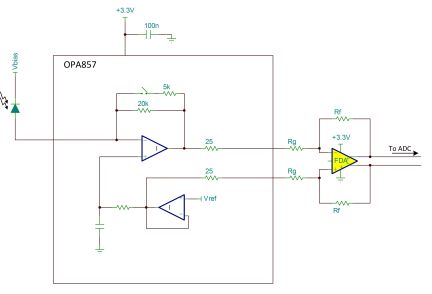
The TIA in our example is a pseudo-differential transimpedance amplifier with the capability of switching between two gains. The two internal transimpedance resistors are 5 kΩ and 20 kΩ. If a 500 Ω load is used, the series resistance of 25 Ω in each output, the overall transimpedance gain becomes 4.5 kΩ and 18.2 kΩ, respectively. Note that the 4.5 kΩ results in the parallel combination of 20 kΩ with a 6.67 kΩ added in parallel using an internal switch. The internal VREF node (Figure 1) is a resistor divider between supply and ground. This VREF node then converts any power glitch into a common-mode signal. The pseudo-differential architecture minimizes the common-mode signal by converting it to a differential error.
The TIA has a 23.4 mA quiescent current when operating of a +3.3-V supply with a worst-case over temperature of 26.8 mA. This information provides both the output voltage and the minimum current drive requirement for defining the power supply and permitting the selection of an appropriate power supply. For now we will not make any assumption as to the nature of the power supply, either a low dropout voltage regulator (LDO) or a DC/DC converter.
Next is the load regulation as it is relatively easy and can be defined without much additional information. The TIA datasheet indicates the minimum load (500 Ω) to ensure performance is not lost. Looking at the maximum output voltage swing, from +1.83 to +0.6 V or 1.23 VP, we can determine the largest dynamic current that the power supply needs to support. In this case the maximum current we can expect is 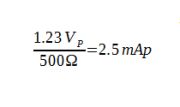
The TIA sources voltage in a fixed resistive load, so the total supply current can vary between 23.4 to 25.9 mA. The TIA average current will be 24.65 ± 1.25 mA or 24.65 mA, ± 5% for a sine waveform operating at full swing. This is a minimal requirement for any power supply load regulation.
Next look at the output noise and PSRR parameters. Before going deeper into those two parameters, have a quick look at the TIA application. A TIA circuit can be designed using any operational amplifiers (op amps). However, designing a high-gain and high-bandwidth signal chain limits the number of amplifier choices. These design considerations on how to select the right amplifier for your TIA application are described in the application note, Transimpedance Considerations for High-Speed Amplifiers. [1]
One conclusion we can take from this application note is that the amplifier’s noise gain increases as frequency increases, significantly degrading SNR. This limits the SNR to a 10 to 30 dB range.
Calculating the root-mean-square (RMS) noise for a given noise power bandwidth (NPBW) normally is done via simulation. It also can be measured directly. This low-noise, 100 MHz bandwidth, dual-fixed gain TIA operates on a +3.3-V power supply. The TIA characterization provides the integrated noise for an 85.7 MHz NPBW of 24.9 nARMS for the 4.5-kΩ gain, and 14.7 nARMS for the 18.2 kΩ gain. Multiplying by the gain, this translates into 124.5 VRMS (4.5 kΩ gain) and 294 µVRMS (18.2 kΩ gain), respectively, at the load.
As a quick reminder, if two sources of noise are uncorrelated, they will add as power. For additional discussion on noise, consult “Noise Analysis for High-Speed Op Amps.” [2]
Calculating noise from two uncorrelated sources is:
Where n1 and n2 are two uncorrelated noise sources.
The nature of the noise differs depending on the type of power supply used. DC/DC converters generate noise as a result of the switching behavior, whereas the LDO generates a thermal and flicker noise. The LDO lets some attenuated noise pass through from the supply at its input [2].
How much degradation can the TIA tolerate from external power supply noise sources? The worst case scenario when using the TIA is when the noise on its output is minimal. The low gain, 4.5 kΩ, corresponds to this minimum noise. For clarity, the total noise degradation is plotted in Figure 2.
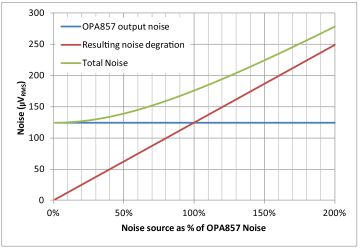
Total noise increases at a faster rate when the added noise source is greater than 20% of the total noise. For an external noise source contributing less than 20% of the total noise, SNR degradation will be minimal at the TIA’s output.
Normally, thermal and flicker noise dominate in LDOs. For this portion, we consider what happens if an LDO powers the TIA. LDOs define noise for a given frequency band (Figure 5). Low noise LDOs, such as the high-performance TPS7A49xx or the low cost TLV71333 are potential candidates. Table 1 makes a side-by-side comparison for both devices.

The output voltage noise varies with the output voltage, noise reduction capacitor, feed-forward capacitance, and so on. In general, noise is calculated for a bandwidth from 10 Hz to 100 kHz. This may or may not be the entire frequency band to consider for a specific application, however, here it is considered as a figure of merit.
Now consider how to define the TIA white noise rejection over the same frequency band to allow simple calculation. The TIA PSRR for the 4.5 kΩ gain is shown in Figure 3.
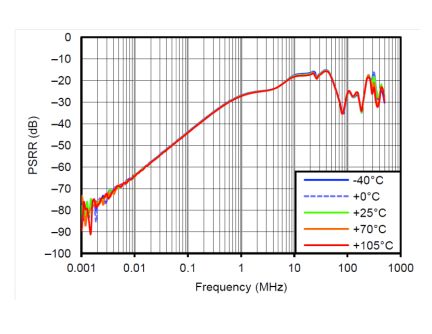
In the 10 Hz, 100 kHz band of interest, this can be approximated to Figure 4.
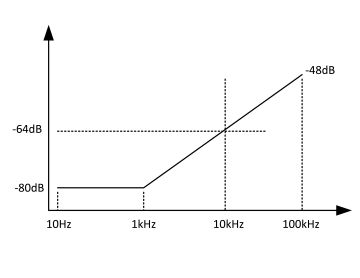
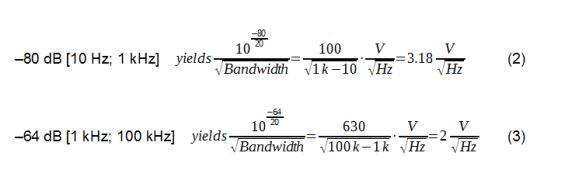
Consider the slope as a first step. The average PSRR from 1 kHz to 100 kHz can be approximated as –64 dB, since we are talking about white noise without any frequency shaping.
To extend the frequency band to 10 Hz, we can go back to the attenuation density of the PSRR to normalize each number over a given frequency band.
The –80 dB [10 Hz; 1 kHz] has a higher density than –64 dB [1 kHz; 100 kHz]. This is due to the reduced band over which the density is calculated.
Because we have an attenuation density, as a first order approximation, an average between the two numbers gives us the average attenuation over the entire frequency band. Multiply the average by the new frequency band, which gives us the attenuation factor (4).
(4)
This corresponds to an average attenuation of –61.73 dB over the frequency range of [10Hz; 100 kHz].
If we do not want the LDO noise to be greater than one percent of the TIA output noise, the LDO noise should be smaller than (5):
(5)
Looking at possible LDOs, this specification does not constrain LDO selection.
Since transimpedance applications often use averaging to increase SNR, noise is decreased by the square root of the number of samples (6).
(6)
With n= number of samples
Let’s consider three different averages of 100, 10 k and 1M. The total output noise decreases by 10, 100 and 1,000, respectively, to 12.45 µVRMS, 1.245 µVRMS and 0.125 µVRMS. The LDO noise is averaged at the same time and profits from averaging.
Let’s turn our focus away from LDO’s and, for now, consider a DC/DC converter driving the TIA . For a light load, the ripple can be approximate as a sawtooth waveform. For a heavy load, a triangle waveform is a better approximation. A sawtooth waveform can be decomposed as a Fourier series and expressed as equation 7 and Figure 5:
(7)
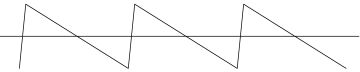
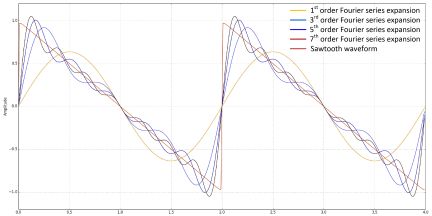
Figure 6 shows the sawtooth waveform approximation with a Fourier series with 1, 3, 5 and 7 harmonics. The fifth-order approximation is sufficient for our purposes. It also has a peak amplitude of 1, simplifying further the algebra as we do not have to normalize the amplitude.
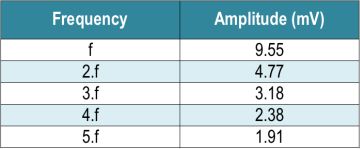
For a 15 mVP ripple caused by a DC/DC converter, the fundamental frequency and the four harmonics amplitude are noted in Table 2.
Next consider what happens when only the TIA is present to reject ripples. Here we are setting the switching frequency of the DC/DC converter to 500 kHz for the discussion. Looking at the PSRR plot in the datasheet, we can fill Table 3 with the TIA rejection and thus calculate the amplitude. In order to have the minimal PSRR, we use the TIA 18.2 kΩ gain.
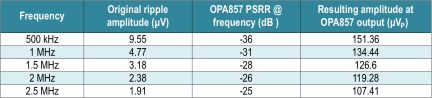
The resulting waveform at the output of the TIA looks like a comb. Figure 7 represents the ripple amplitude at each frequency before and after the TIA.
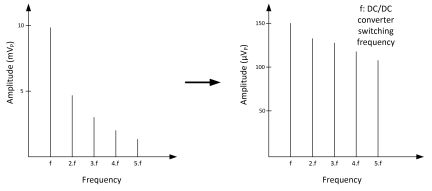
If more tones were present, the time domain equivalent would be a sin(x)/x function. Due to the limited number of harmonics being looked at, the time domain waveform looks like a pulse (Figure 8).
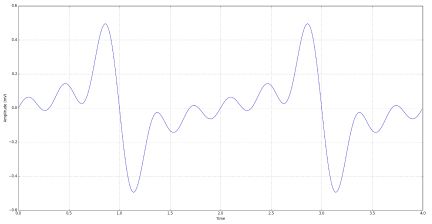
The result is an undesirable ~1 mVPP signal that can be detected as a fake pulse in many TIA applications, especially in applications that use averaging to increase the system’s dynamic range.
Note that the TIA PSRR reduces the 30 mVPP signal to 1 mVPP. With 20 kΩ internal gain, this represents an error of 50 nAPP at the input. This is four times the RMS noise and must be reduced to an acceptable level for the system to function properly. The best approach is to use an LDO. Averaging here does not result in any ripple reduction as the ripple does not change over the sampling period. The question now becomes: What minimum PSRR should the LDO have?
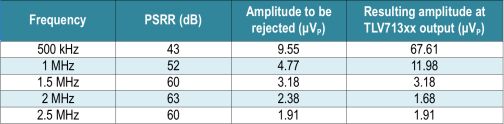
From the noise analysis, we know that the overall noise will be degraded by two percent, if the added disturbance corresponds to 20% of the noise value. If we set the ripple amplitude to be 127 µVP or 254 µVPP, this ensures that in any gain configuration, the total noise degradation will be less than 2%.
To attenuate a signal from 30 mVPP to 254 µVPP, we need more than 41.5 dB of PSRR in the power supply from the switching frequency of 500 kHz to at least five times the switching frequency, if the previous model is used. If we consider this as a first-order approximation because the PSRR does not change with output voltage for LDOs, we use the data available in the datasheet to solve our problem. From this approximation, we can conclude that the amplitude can be reduced to 173 µVPP (Table 4).
Starting with the low-cost LDO, let’s analyze the different power supply solutions. With more than a 1.2-V dropout a linear regulator may be a solution for filtering a 500 kHz ripple originating in the DC/DC converter. However, rejection between 500 kHz and 2.5 MHz comes mostly from the bypass capacitor and board parasitic. This can be layout-dependent and vary significantly from one layout to another. The PSRR for the low-cost LDO is shown in Figure 9.
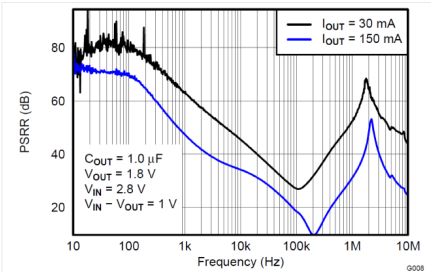
Many LDOs, such as the TLV713, do not work well in this application. When trying to apply lower voltage data to higher voltage, here 1.8 to 3.3 V, remember that the error amplifier loses loop gain with increasing output voltage. In this case, the 1.8-V PSRR numbers must be derated for the +3.3-V output voltage LDO, further degrading PSRR.
A high-performance solution LDO, such as the TPS7A4901, actively maintains a high PSRR and depends less on the output capacitance and layout. Even with a reduced capacitance of 2.2 μF instead of 10 μF, it offers sufficient PSRR, allowing capacitor variation over temperature. Reducing the switching frequency to 100 kHz or 200 kHz instead of 500 kHz also increases the margin and ensures that the ripple from a DC/DC converter is not a problem in the end system. The PSRR for a high-performance LDO is shown in Figure 10.
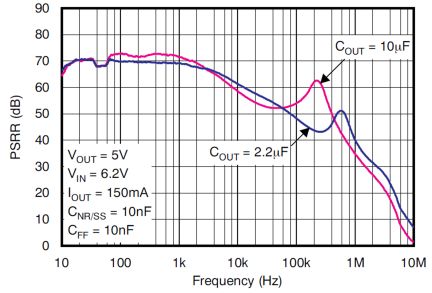
The power chain is almost complete at this point, with a DC/DC converter operating ideally at 100 kHz to 200 kHz, followed by the LDO with adequate bypassing to power the TIA. The last parameter to look at is the line regulation. In this case, the line regulation is dependent on the DC/DC converter and its total load.
References
1. Ramus, Xavier. Transimpedance Considerations for High-Speed Amplifiers, TI Application Report (sboa122), November 22, 2009
2. Noise Analysis in Operational Amplifier Circuits. TI Application Report (slva043), 2007
3. Pithadia, Sanjay. LDO Noise Demystified, TI Application Report (slaa412), June 2009
4. Download these datasheets: OPA857, TLV71333, TPS7A4901

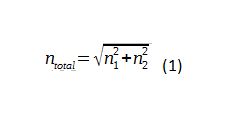
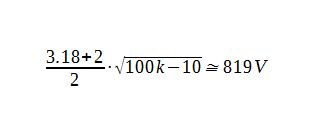
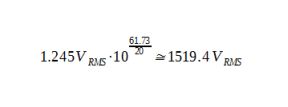
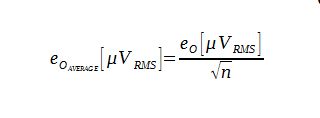
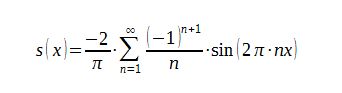

Leave a Reply